数学 、特に 初等解析学 における(狭義の) 一次関数 (いちじかんすう、 英 linear function )は、( 一変数 ( 英語版 ) の)一次 多項式関数 ( firstdegree polynomial function )、つまり 次数 1 の 多項式 が定める 関数近似式 1次近似式: 3次近似式: 5次近似式: 7次近似式: のグラフと近似式のグラフ グラフの作成は,ASCIIsvgを用いている。ASCIIsvg コマンドとJavaScriptを変更して更新ボタンを押すと,グラフが変更される。 入力 (ASCIIsvg コマンド と JavaScript) 参照ページBはその一次式を利用して三 次元データを得るために恐竜 の足跡化石を撮影したもので ある。 Aについては一次式を正確 に求めるために,等倍で高さ が増加する目標物として厚さ 約7mmの発泡スチロール板を 恐竜の足跡化石の高さの最高 点以上になるまで,階段状に 47段積み重ねて撮影した

一次方程式 移項を使う問題の解き方と文章題のコツ リョースケ大学
一次式とは
一次式とは- 例:如图已知某一次函数的图像交X轴于点(1,0),交y轴于点(0,2),求这个一次函数的解析式。 解:首先设这个一次函数的解析式为y=kxb(k≠0), 把图像上的两点带入可得0=kb,2=0b 解得k=2,b=2 所以这个一次函数的解析式为y=2x2其中, 是二次项, 是一次项, 是常数项。 是一个重要条件,否则就不能保证该方程未知数的最高次数是二次。当然,在强调了是一元二次方程之后, 也可以省略不写。當然,一元二次方程式有時會出現虛數根。 歷史 古巴比伦留下的陶片显示,在大约公元前00年(00 BC)古巴比伦的数学家就能




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
一次式であらわせる式でも、文章題などの応用問題では変域が存在する。 たとえば 窓があります。窓の高さは90 cmとします。窓を x cmあけたときの、あけられた部分の面積 y (単位はcm 2 とする)は、いくらでしょうか? という問題では、 y = 90x と式で表せるが、 窓のあけられた長さを0より1次方程式を解くとは 3x5=−1 (1) のように未知数 x を含む等式を x についての方程式といいます。 この頁では、1次方程式から「等式の性質」を使って解を求める方法を学びます。 x=··の形をした式を解といいます。一次式で表わすことができるようである しかも著者 らの条件では比較的短時間 (25min) で塗膜内の残留ひ ずみ (応力) は無視できる程度に下がってしまう性質が 見られる 一方, 木材の creep 変形は短時間領域では, 近似的 に時間の対数の一次式で表わすことができるから, 塗 膜内の応力は
トリックスであることを利用すると,式 (1) は各 節点自由度ごとの一次式に分解できることが容易に 証明できる.その後陰解法と同様の離散化を行なう ことにより, m 直州 =P 州— F 刑 (2) を得る.ここで添字 iは 番目の節点に関する式で あることを表わしている F は節点 iにかかる内力 で未知数 の最高 次数 が1である式。 出典 小学館デジタル大辞泉について 情報 凡例 有一条解析式很恶心的曲线 ,我可以用多项式仿造一条曲线 , 例如只做了一次 近似的话, 近似的多项式和原始函数是通过同一点 的。 若进行二次近似, 近似的多项式和原始函数既过同一点,而且在同一点的导数相同,也就是多项式表达的函数在 点的切线也相同。 类似进行三次近似的话,不
1つおきの漸化式 a n2 =f(a n) 推測型の漸化式(数学的帰納法で証明する最終手段) 相似な図形の数列と漸化式;一次因式提出公因式 在一个公式内把其公因子抽出, 一般 会得到,例子: 7 a 98 ab 其中,7 a 是公因子。 因此,提出公因式后得到的答案是:7 a (1 14 b ),这两个因式都是一次因式。 7a^214a^2 其中,7 a^2 是公因子。 因此,提出公因式后得到的答案是:7 a^2次の問題を例にして考えていきましょう。 例 x 2 5x8をx2で 手順1を行うと、3x8という式が残る。 残った式に対しても手順1と同じことをする。 xを3xにそろえるために、割る数全体を3倍する。 3(x2)=3x6 先頭の項がそろったら、割られる数から引き算をする。 割れなくなるまで手順1を




一次方程式とは 慶應生が解き方3ステップ教えます 問題 文章題付き 高校生向け受験応援メディア 受験のミカタ




中1 1次方程式 でつまずく原因と解決法 導入
対応完了までの間、ご利用の際は恐れ入りますが、お使いの教科書等と照合して内容をご確認の上、用途に合わせてお使い頂きますようお願い致します。 21年4月9日 株式会社パディンハウス ツイート 中学1年生で習う簡単な一次式の乗法、除法、加法 列一元一次方程的技巧 —— ①弄清题意,找出未知数并用x表示②找出应用题中数量间的相等关系,列方程③解方程④检查,写出答案一元一次方程指只含有一个未知数、未知数的最高次数为1且两边都为整式的等式一元一次方程只有一个根一元一次方程可以等式の性質を利用します。係数に少数・分数をふくむ1次方程式は,両辺に同じ数 をかけて,係数を整数にして解きます。少数の場合は10,100,を,分数の場合 は分母の最小公倍数をかけます。 等式の性質 a=bのとき,①a+c=b+c ②a-c=b-c ③a×c=b×c ④a÷c=b÷c(ただし,c≠0) ま
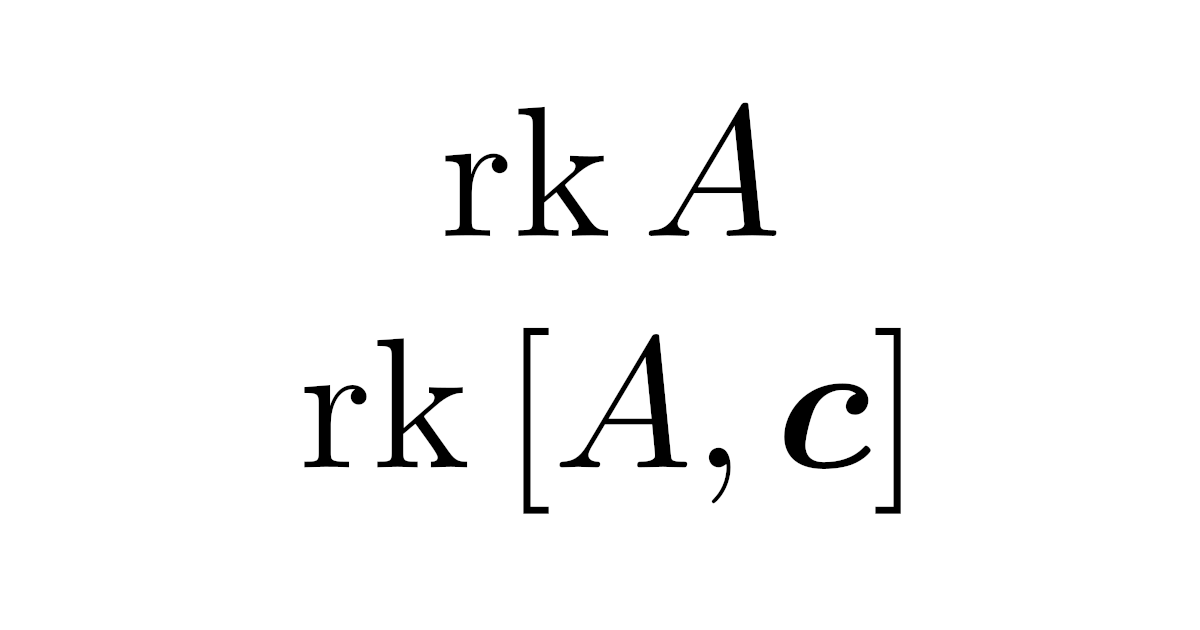



連立1次方程式が 解をもつ条件 と 解の自由度 の考え方




項 係数 一次式とは 中1数学 Youtube
97 「線形」は一次式、「非線形」はそれ以外 第10章「微分方程式」のエッセンス(定数変化法) 101 「微分方程式」の分類 102 「非斉次」には「定数変化法」 103 「空気抵抗」のある物体の落下 第11章「ポニーテール」を華麗に揺らす方法小数や分数を含む方程式に関しては、手順1の前段階に当たる 手順0 ともいうべき一 工夫が必要になります。 手順0とはどんなものか。 一緒に確認していきましょう。 小数を含む方程式の手順0 小数を含む方程式の手順0 小数を消すために両辺を10倍、100倍する。 問題 次の方程式をEnjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on




スタディピア 1次方程式



一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス
这样我们就得到了一元二次方程的求根公式。 一元二次方程判别式推导 现在,我们已经得到了求根公式。方程的两个根的唯一区别就是后面的根号下b²4ac,一个是,一个是。那么我们要判断这两个根的情况,就要令Δ= b²4ac来进行比较。 最高の次数は1だから、こいつは一次式ってわけなのさ。 ってことで、 移項や同類項が終わって次数を数えてみよう! まとめ:二次方程式は最高の次数が2の方程式のこと! 二次方程式の正体もわかったかな?? 簡単にいうと、 二次式をふくむ方程式。 もっとわかりやすくいうと、 移項三元一次方程式 三元一次方程式在线计算器 x y z = x y z = x y z = 结果 x = y = z = 本在线计算工具解决了3个未知变量的代数运算。每个方程含有未知变量x,y和z。这三元一次方程未知计算器计算的变量x和y的输出值的输入值x,y和z系数;在数学计算中,有许多情况出现在使用含有3个未知



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点




一次方程式の解き方 いろいろな計算練習 無料で使える中学学習プリント
一元一次方程式也被稱為线性 方程,因為在笛卡尔坐标系上任何一個一次方程的圖形都是一條直线。 组成一次方程的每一项必須是常数或者是一个常數和一个变量的乘積。 且方程中必須包含一个變量,因為如果没有變量只有常數,式子則是代数式而非方程式。 如果一次方程式中只包含一个文字符この記事の内容 識別子は、整数、 float 、 enum 、 struct 、 union 、配列、ポインター、または関数型を持つことができます。 識別子は、オブジェクトの指定として宣言された場合 (その場合は左辺値)、または関数として宣言された場合 (その場合は関数指定子 このページは、 中学1年生で習う「小数の一次式の加法(足し算)の問題集」が無料でダウンロードできる ページです。 この問題のポイント ・小数の一次式同士の足し算をします。 ・かっこをはずして、文字がある「一次の項」と、「数の項」を同士を




一次方程式の解の求め方 数学fun




連立二元一次方程式をいろいろな方法で解いてみよう 身勝手な主張
21年6月9日 このページは、 中学1年生で習う「分数の一次式の項をまとめる問題集」が無料でダウンロードできる ページです。 この問題のポイント ・分数の一次式について「一次の項」や「数の項」をまとめて簡単にします。 ・分母が違う分数の動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru一元一次式未知數的位置 一個一元一次式的未知數 不可以在 分母 ,但是 可以放在分子 。如: 不是一元一次式,但 是一元一次式。 不可以 有一個以上不同 的未知數。如: 不是一元一次式。




連立3元一次方程式でこのように詰んでしまいます Clear




中学1年数学 一次方程式 移項とは なぜ符号が変わるのかまでしっかり理解 数学の面白いこと 役に立つことをまとめたサイト
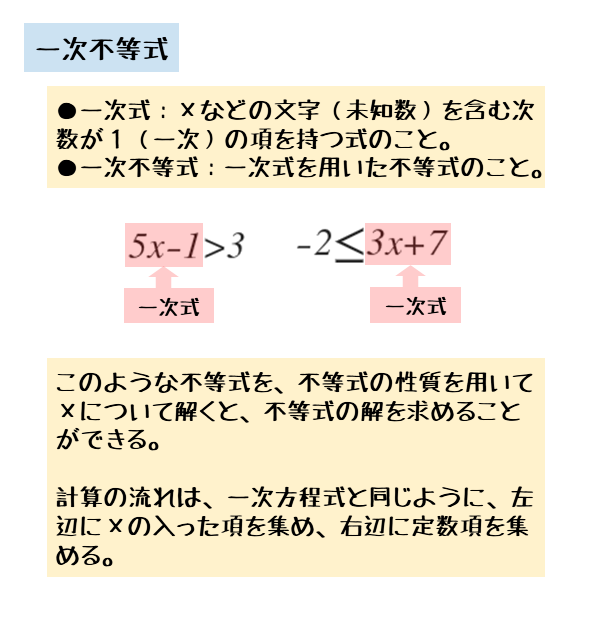
不等式の性質 a < b ならば ac < bc , a−c < b−c a < b, c > 0 ならば ac < bc , a c < b c a < b, c < 0 ならば ac > bc , a c > b c 不等式では両辺に同じ負の数をかけたり、割ったりすると 不等号の向きが変わる 。違う種類の一次式がかけられたものと、同じ一次式が二乗されたものです。 次の例題で分解方法を確認してみましょう。 例題1 まずは公式\((1)\)を使った例です。例題として以下の式を部分分数分解してみたいと思います。 $$\frac{x2}{x(x1)}$$不定積分の漸化式 → 携帯版は別頁 分数関数(有理関数)の不定積分 (例題中心) はじめに・目次 この頁で取り扱う不定積分 この頁では次の (1)~ (3), (A) (B)について解説と例を示す.実際の不定積分の計算においては (A) (B)を先に考えて, (1)~ (3)で




中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト




中学数学 移項と様々な1次方程式 中学数学の無料オンライン学習サイトchu Su
ゆえに非斉次方程式系の解の一つ(特殊解)と随伴斉次方程式系の一般解により、非斉次方程式のすべての解を記述することができる。つまり、 x 0 が A x = b の特殊解であるならば、非斉次方程式の解の全体は = { =} で与えられる。これは ker A に随伴したアファイン空間であり、やはり方程式x の前の数 2 を 係数 といいます。 また、項 2x=2x 1 の次数は 1 次で、項 -5=-5x 0 は0次なので、この多項式は 1次式 です(最大の次数で表します)。 多項式 2x 2 -3x+4 は、2x 2 と-3x と4 の3つの項からできています。本論文では,2次 元弾性問題を変位法を用いて解析を行つた場合の離散化誤差を検討する。Walz, Fulton, Cyrus2)は,各 節点における力の平衡方程式が,平 衡を考えている節点とその隣接節点における変位の一次式と




誰でもわかる数学 中学1年 一次方程式の解き方 Youtube



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく
1次方程式 axb=0 の解とグラフを求めます。 一次方程式 \(\\ a b 一次方程式 axb=0 の解 お客様の声 アンケート投稿 よくある質問 リンク方法 一次方程式の解 110 /17件 表示件数 1 1845 歳未満 / 小・中学生 / 役に立たなかった / 使用目的 問題の答え合わせ ご意見・ご 二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解二元一次方程组的解:二元一次方程组的两个公共解,叫做二元一次方程组的解。 标准二元一次方程组包含六个系数,两个未知数,形式为: 式1,axby=c 式2,a2xb2y=c2連立漸化式 a n1 =pa n qb n 、b n1 =ra n sb n;




中学数学1年 1次方程式の利用 整数 受験の月



数と式 一次不等式について 日々是鍛錬 ひびこれたんれん
A, bは 定数 (整数や分数などの数字)なので、その数を求めれば1次関数の式が出る。 1次関数の式の出し方は大きく分けて 2通り 。 ・傾きと1点から出す方法。 ・2点から出す方法。つまり、二次反応では濃度の逆数を取ってプロットすれば直線関係となる。 零次反応 A→P 反応次数が0なので、次の式に従う。 v = k このとき、初濃度をC 0 、反応した後の濃度をC、経過時間をtとすると次の式によって表わすことができる。 C = C 0kt B (x) B(x) B (x) が一次式(特に一次の係数が1 )のときは組立除法を使うとさらにスピーディーにできます。 最後に例題をもう一問。 例題2 A (x) = − 2 x 4 A(x)=2x^4 A (x) = − 2 x 4 を B (x) = x 2 − 1 B(x)=x^21 B (x) = x 2 − 1 で割った商と余りを求めよ。 方法1による解答: 商は二次式,余りは一次以下の式




中学数学 22 1次式の加法 減法 Youtube




中学1年生 数学 無料問題集 一次方程式 おかわりドリル
1次分数型の漸化式 a n1 =(pa n q)/(ra n s) 隣接3項間型の漸化式 a n2 pa n1 qa n =0;今回のまとめ 1次結合とは一つのベクトルを他のベクトルの組み合わせで表すこと 1次独立と1次従属は方程式を満たす定数が全て0かどうかの違い 簡約化を使って1次独立か1次従属かを調べることができる 今回勉強してきた内容は今後も登場してくるし




この三元一次方程式の解き方を教えて下さい Clear



U9j580gf8iba369ji2w Xyz P 377




中1 数学 式を簡単にする 一次式の加法 減法 無料学習プリント教材




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




一次式の乗法や除法 文字でもルールは掛け算と割り算と同じ 中学や高校の数学の計算問題




例題 連立3元1次方程式の解き方 Youtube




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト



数学1年
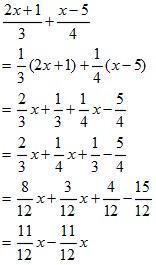



Math 1次式の計算 分数式の計算の指導法を考える 働きアリ




中1 1次方程式 でつまずく原因と解決法 分数




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Studydoctor項 係数 一次式とは 中1数学 Studydoctor



中3 二次方程式の基本解説 中学数学の方程式 中間 期末テスト 高校入試対策




一次方程式 Wikipedia




一次式の加法や減法 文字の前の数を足したり引くだけ 中学や高校の数学の計算問題




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




1次式の積 数学i フリー教材開発コミュニティ Ftext



第1章 連立方程式




一次方程式とは チーム エン




一次方程式と一次不等式の違い 看護受験の必須 数学の公式を確認テスト Vol15 Kazアカデミー 大阪の看護学校 看護予備校




一次方程式の解 計算ドリル 問題集 数学fun



1
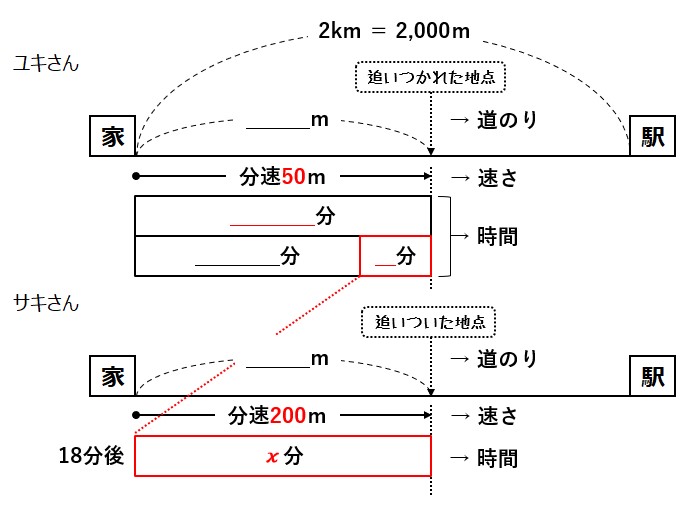



わかる 中学数学 一次方程式の利用 文章題 道のり 速さ 時間の問題 を丁寧解説
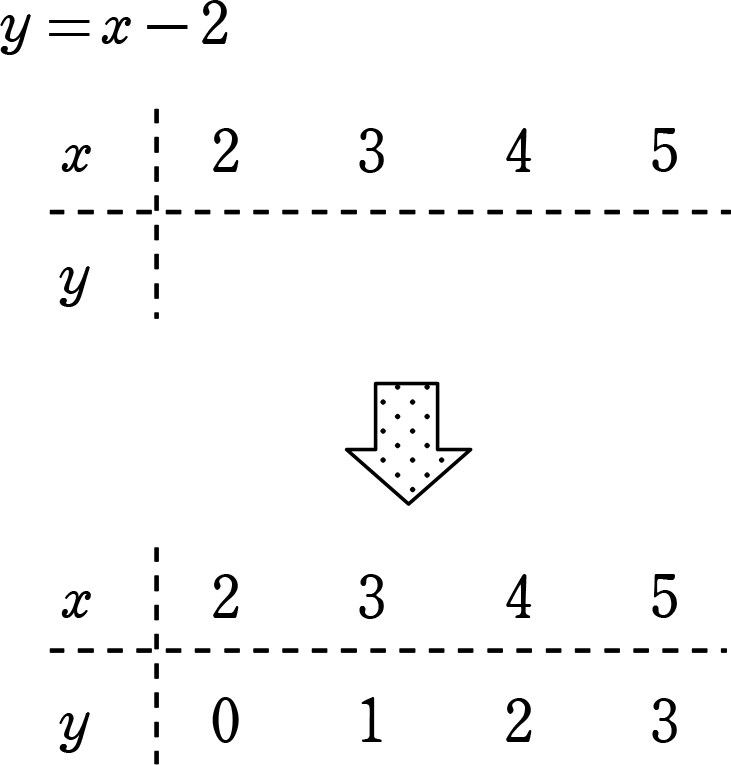



中学数学 連立方程式 二元一次




一次方程式 移項を使う問題の解き方と文章題のコツ リョースケ大学



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点




2 で X Yの一次式の積となるための条件はd Clear




一次方程式とは 簡単に理解しておこう 方程式の解き方まとめサイト



数学1年




5分で分かる 中学数学 035 1次式と数の乗法 除法 Youtube



同次連立一次方程式



数学 公式集 連立一次方程式



一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス
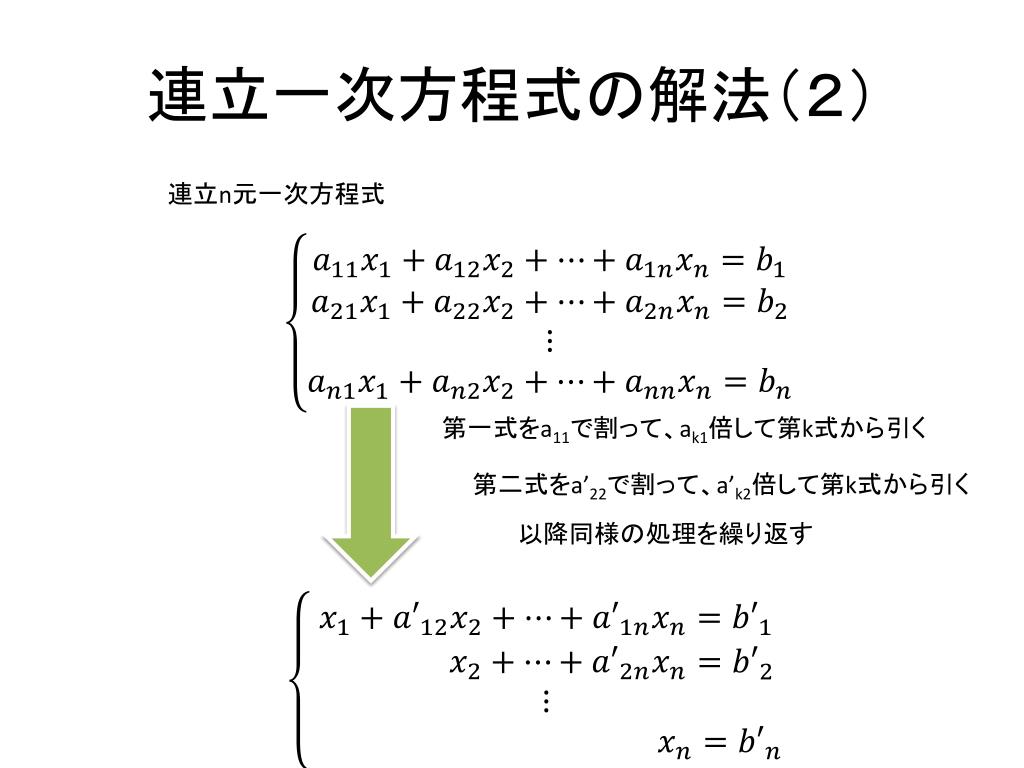



Ppt 連立一次方程式の解法 1 Powerpoint Presentation Free Download Id




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




中1 一次式 項 係数 まとめ 中学生 数学のノート Clear



3




中学数学1年 1次方程式の利用 分配と過不足 受験の月




中学1年生 一次方程式の解を求めよう 学童cafe チャイルドスペース




かずお式中学数学ノート3 中1 一次方程式 Amazon Com Books
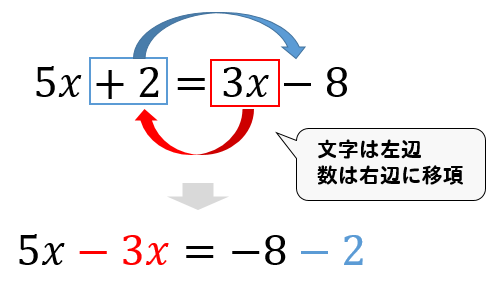



一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト




まる先生 一次方程式と二次方程式のグラフは どんどんかきこみをする まる練 自宅学習 家庭学習 テスト対策 テスト勉強 マンガで勉強 高校入試 高校受験 まる練数学 一次方程式 二次方程式 グラフ



3




Xについての一次方程式 ー3分の1x 4 Xの計算方法を教えてください 数学 教えて Goo
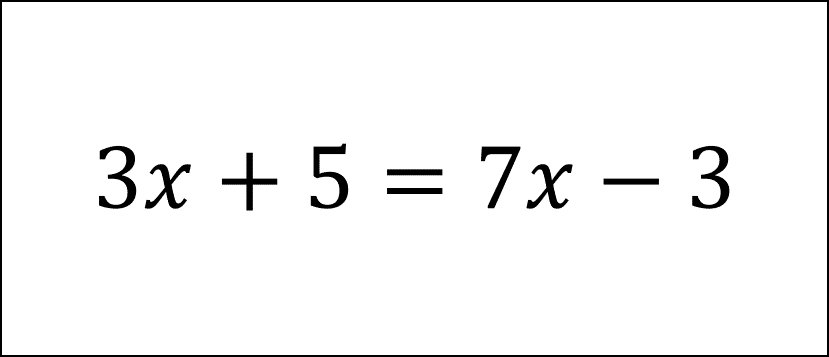



1次方程式でケアレスミスを減らすテク みんぷり 無料で自由に使える学習プリント




一次式と数の乗除 文字式と数の分配法則のルールを覚えよう 中学や高校の数学の計算問題




数学 中2 35 二元一次方程式のグラフを書く Youtube



一次方程式の解き方をめちゃくちゃ分かりやすく解説してください Yahoo 知恵袋




項 係数 一次式とは 中1数学 Youtube




連立一次方程式とは コトバンク



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策



1




かずお式中学数学ノート3 中1 一次方程式 Amazon Com Books




1次方程式の解き方 1 無料で使える中学学習プリント




一次方程式 分数があるパターン Youtube




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




不定解の連立一次方程式 掃き出し法 単位の密林




図形の規則性から一次方程式を立てる 中学数学 理科 寺子屋塾の復習サイト
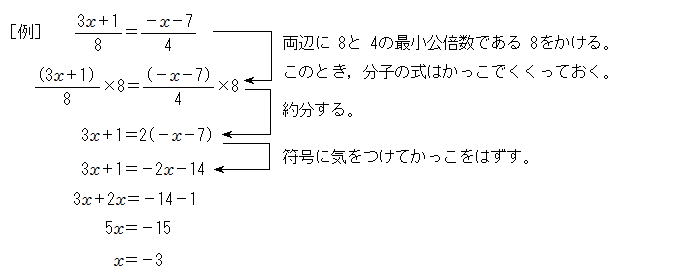



1次方程式 分数がある1次方程式の計算 中学数学 定期テスト対策サイト




一次多項式 Sanichda1 1




中学1年生 数学 無料問題集 一次方程式 おかわりドリル
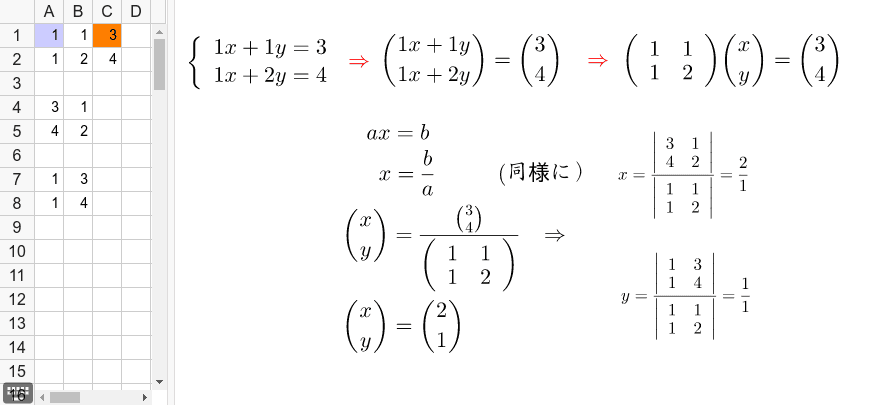



二元一次連立方程式 Geogebra




中学数学 一次方程式
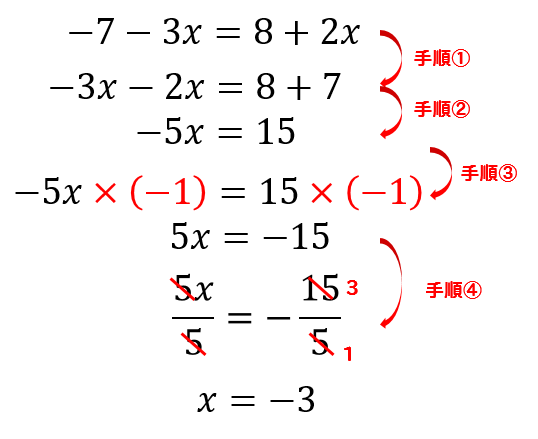



中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



一次方程式の問題や文章題の解き方を例題で詳しく解説 Studyplus スタディプラス
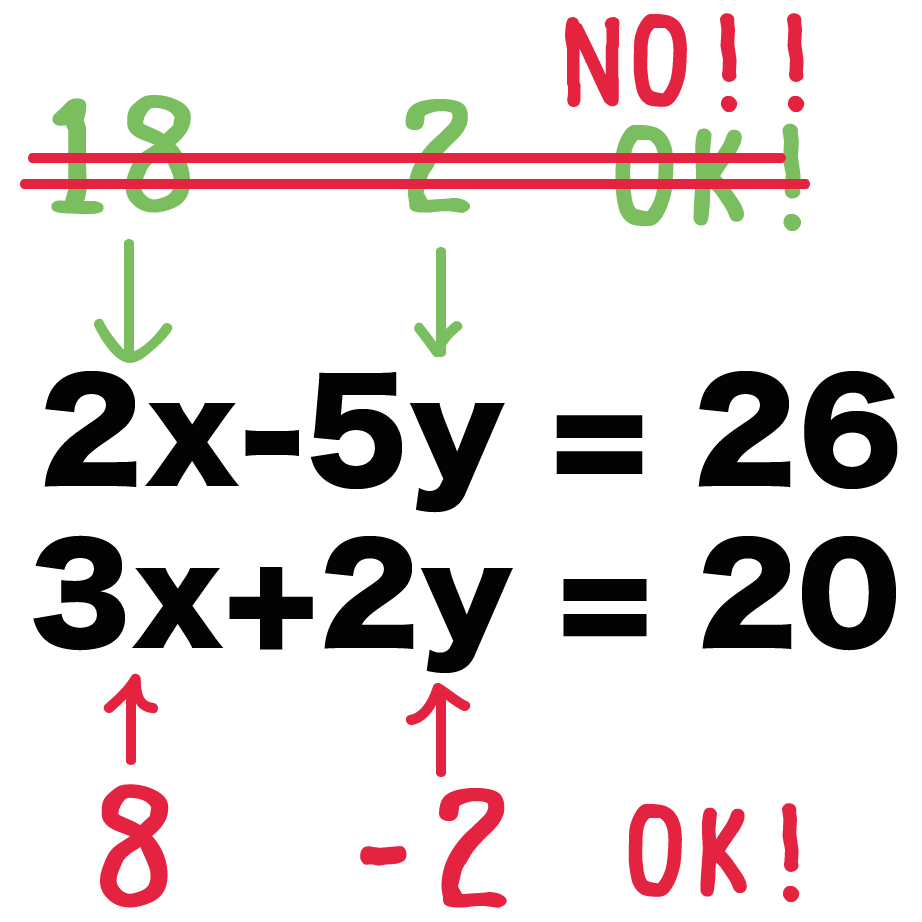



連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




1次関数と2元1次方程式の違い Youtube
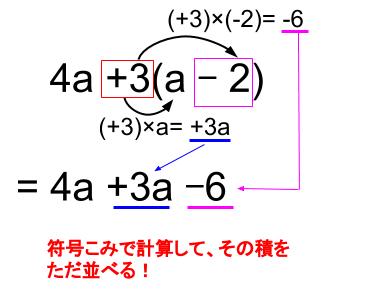



分配法則 1次式の計算 中学数学の無料オンライン学習サイトchu Su



中1 一次方程式のかっこは外してから解こう 中学数学の方程式 中間 期末テスト 高校入試対策




一次方程式 連立方程式 ルートの計算




スタディピア 1次方程式
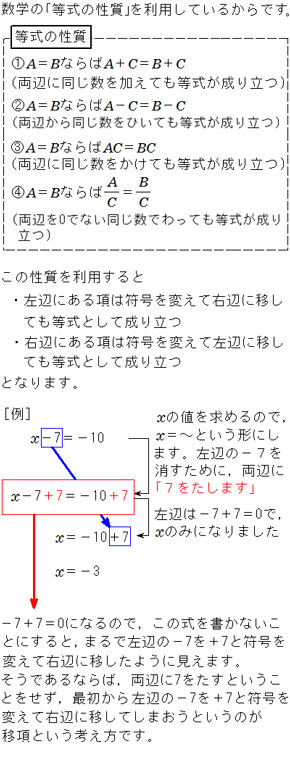



1次方程式 なぜ移項するとき符号がかわるのか 中学生からの勉強質問 数学 進研ゼミ中学講座



2




この式は一次式ですか それとも一次式ではありませんか Clear




中1 いろいろな一次方程式 中学生 数学のノート Clear




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




1次式の加減法 カッコの前にマイナスがある時は解き方に注意 中学や高校の数学の計算問題




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




高校数学で学習する連立方程式の解き方まとめ 数スタ



中学数学なら数学わかルート 無料動画で学ぶ



0 件のコメント:
コメントを投稿